Identifying a pattern - Math Accomplished

Today, I want to talk about identifying a pattern, which is a very common method of problem solving.

Look at the picture below. Given the first six squares, can you describe the pattern and find the sum of the areas of the first nine squares in this sequence?

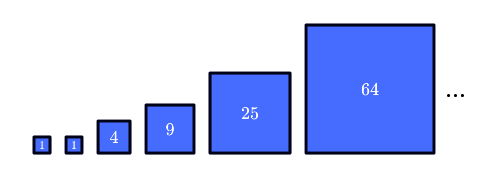
As it often goes with sequences that follow a pattern, our first step is to try and find the dependency between consecutive terms. The first two squares are identical. Let's look at the third square. It has an area of 4. What is the possible dependency between 2 and the previous terms (elements) of the sequence? Previous terms had areas of 1. How can we get 4 from 1 and 1? Maybe we add 1 + 1 and double the result. Let's make a conjecture that the area of the next term is twice the sum of the areas of two previous terms: 2 (1 + 1) = 4

Next step is to check the conjecture with the next term. The next term (element) in the sequence is a square with an area of 9. Does it fit our conjecture? Twice the sum of the areas of two previous terms, 2 (1 + 4), is not 9. Our conjecture was wrong. Finding that a conjecture is wrong is useful. We can rule it out and try something else.

How else the square with an area of 4 can relate to two squares with the areas of 1? Smaller squares have a side length of 1, and the larger square has a side length of 2. How can we get 2 our of two 1s? We can add them: 1 + 1 = 2. Our next conjecture is that the length of the side of the next square is the sum of the lengths of the sides of two previous squares.

Let's test it. The 4th term is a square with an area of 9 and the side length of 3. The sum of the lengths of the sides of two previous squares is 1 + 2. It does equal 3. What about the 5th term? 2 + 3 = 5. It works. You can also check the 6th term to be sure.

We found a pattern. By the way, you might have recognized it as famous Fibonacci numbers. If you have not, you can find out more about Fibonacci numbers on Wikipedia. Squares with sides that follow the Fibonacci sequence can be arranged as adjacent rectangles in a continuous fashion:

To find out the sum of the areas of the first nine squares, we do not need to draw all of them (they get really large!) Instead, we will make the sequence of numbers:

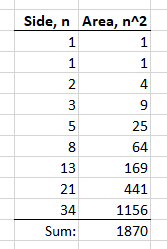
For this example, I used Excel. On the exams, you can use a scientific calculator such as TI-84 or Nspire CX II to create lists of data. The elements of the first list are composed of Fibonacci numbers (each subsequent term equals the sum of two previous terms) and the second list is composed of their squares.