Balancing The Scale

(read more on Brilliant)

Balancing the scale is a type of a mathematical puzzle where we have various shapes or symbols on the scales that need to be balanced, meaning that their "weight" should be equal.

Can you balance the 4th scale on this picture?

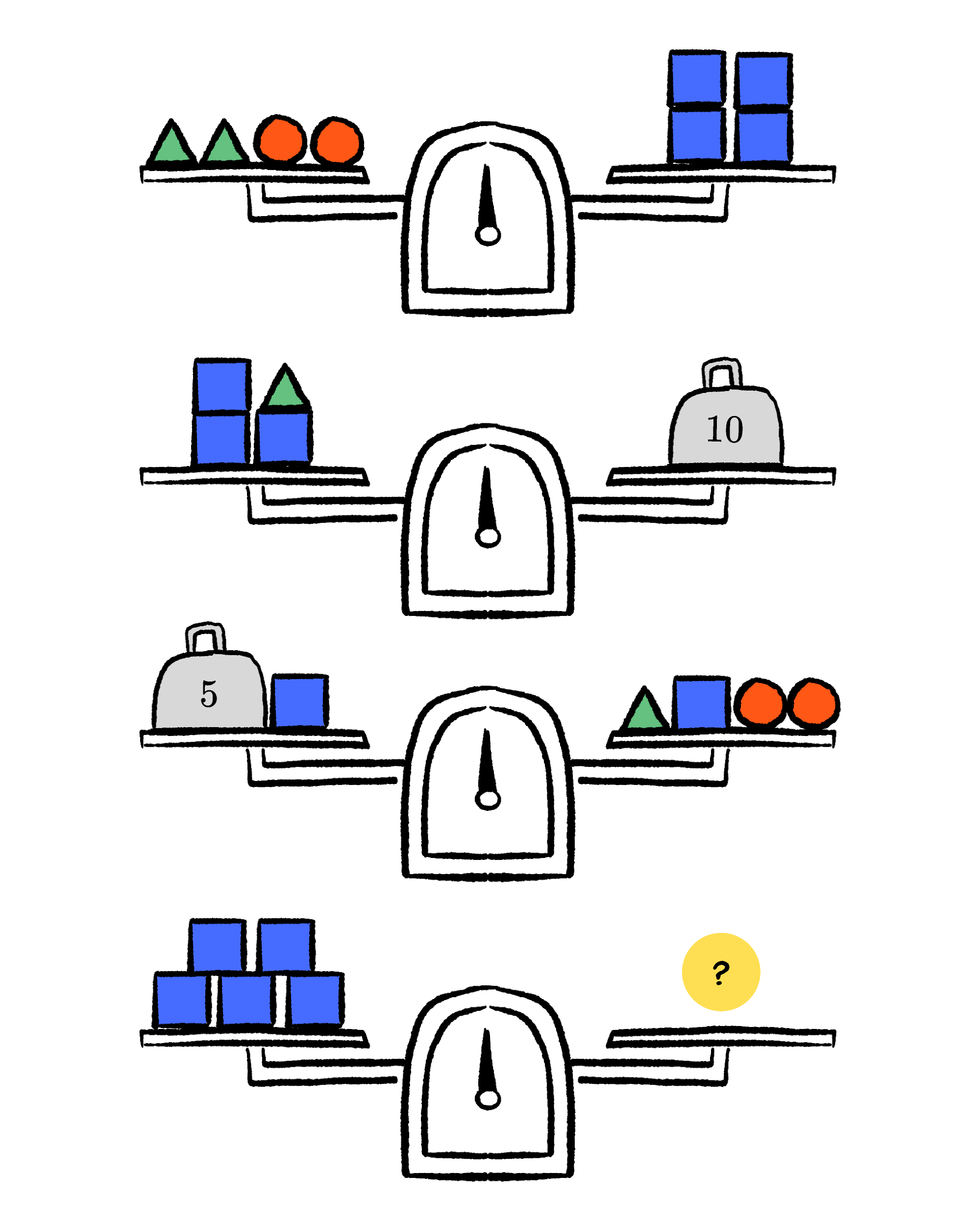
Here, we have shapes of three different types: green pyramids, orange balls and blue blocks.

The most common strategy is to express each scale as an equation with different variables and use substitution or elimination to find the value of the target variable (that would  be the blue blocks in our case). Let's try!

Let blue blocks be the variable x, green pyramids be y, and orange balls - z. What do we have?

(1) 2y + 2z = 4x, therefore, 2y + 2z - 4x = 0

(2) 3x + y = 10 lbs, therefore, y = 10 - 3x. We isolated y, expressing it through another variable, x.

(3) 5 + x = y + x + 2z, therefore, y + x + 2z - 5 - x = 0 and y + 2z - 5 = 0

Let's combine (1) and (3) to get rid of the variable z:

(1) + (3):

2y + 2z - 4x = y + 2z - 5

2y - 4x = y - 5, therefore, y = 4x - 5

We now have two expressions of y:

y = 10 - 3x and y = 4x - 5

Let's put them together and find x:

10 - 3x = 4x - 5, therefore, 15 = 7x and x = 15/7

Therefore, one blue block weighs 15/7 of a kilo. It is 2 kg and 1/7th. The weight of 5 blue blocks then will be 10 5/7 kg.

What if you were asked to balance the weight of 5 blue blocks with other shapes? Let's find out how much each of them weighs.

From y = 10 - 3x: 

y = 10 - 45/7 = 25/7. One green pyramid weighs 3 4/7 kg.

From 2y + 2z = 4x:

2z = 60/7 - 50/7 = 10/7, therefore, z = 5/7. One orange ball weighs 5/7 kg.

Five blue blocks, which weigh 75/7 kg, can be balanced with various combinations of pyramids, balls, and weighs. For example, with two green pyramids and five orange balls. What other combinations can you find?