Cryptograms
(Find out more on Brilliant)
Level: Advanced.
In a cryptogram, letters stand for numbers. Can you find the value of T in the example below?
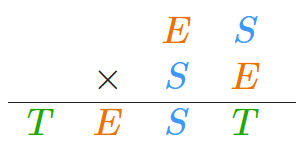
Facts:
- E, S, and T, as starting digits of a number, cannot be zero.
- Carry over: Remember that when the product of multiplication is two digits, the leftmost (the tenth) is carried over to the next position to the left.
- Analyzing digits: If we follow the vertical multiplication procedure step by step, we will find the following and can make various conjectures, e.g. that neither S nor E can be equal one; that the last digit of their product is T, etc.
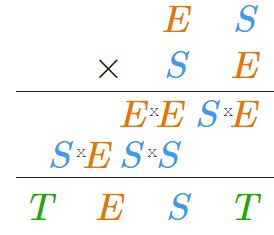
- Equations:
ES x SE = TEST
TEST = 1000 x T + 10 x ES + 1 x T = 1001 x T + 10 x ES
Therefore, ES x SE = 1001 x T + 10 x ES.
Isolate 1001 x T:
1001 x T = ES x SE - ES x 10
1001 x T = ES (SE - 10)
We know that ES is a two-digit number, and SE - 10 must be two-digit as well.
* Why it cannot be a single-digit number? See how S x E is not equal to either S or E? It means neither S nor E is equal to one. Therefore, SE is at the very least 23, and 23 - 10 is not a single-digit number.
Let's factor out 1001:
1001 = 7 x 11 x 13
1001 x T = ES (SE - 10) = 7 x 11 x 13 x T
ES, as a two-digit number made of different digits neither of which is 1, cannot be 7, 11 or 13. It is therefore a multiple of some of these factors.
Can it be a multiple of 11? It cannot, because two-digit multiples of 11 are all made of the same digits (e.g. 22, 33...)! Therefore, it is (SE - 10) that must be a multiple of 11. What can it be?
(SE - 10) can be 22, 33, 44, 55, 66, 77 or 88. That would make possible SE of 32, 43, 54, 65, 76, 87 or 98.
Therefore, possible ES are 23, 34, 45, 56, 67, 78 or 89. Which of these are multiples of 7 or 13? The possibilities are 56 and 78. However, 56 can be excluded because 5 x 6 = 30, with the last digit of 0, and the last digit T cannot be 0 (the four-digit result cannot start with zero).
By elimination, the only option that works is ES of 78. 7 x 8 = 56, and the last digit, T, must be 6.
The answer is 6.


