Factorization: Rectangle within

(more on Brilliant)

Four right triangles are put together to form a rectangle. All triangle side lengths are integers. Can you find side x of the rectangle in the center?

Strategy: We will use factorization to find possible side lengths.

The formula of the area of a triangle is:

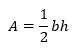
In a right triangle, one of the sides is the altitude, and the area of a right triangle is one half of the product of the lengths of its sides.

Let's look at the larger triangle, with an area of 150.

150 is one half of the product of the lengths of two sides of the triangle, and both sides have integer lengths. We can find all possible integer lengths by factoring a number. What number is it?

If 150 is one half of the product, the product is 150 * 2 = 300.

Integer factors of 300 are: 2 * 2 * 3 * 5 * 5.

At least one of these numbers is the length of one of the two sides of the triangle. Possibilities are:

2 * 150

3 * 100

4 * 75

5 * 60

6 * 50

10 * 30

12 * 25

15 * 20

Since we know that the third side - the hypotenuse - must also have an integer length, we can rule out all possibilities except 15 * 20.

Now, let's look at the smaller triangle which area is 96.

If 96 is one half of the product of the lengths of two sides, the product is 192.

Notice that, according to the picture, the larger side of this triangle is 1 more than the smaller side of the other triangle. Therefore, it is 15 + 1 = 16.

If 16 times the length of the other side is 192, the length of the other side is 12. You can also check that the triangle with the sides of 12 and 16 does indeed have an integer hypotenuse, 20.

Therefore, x is the difference between 20 and 12.

The answer is 8.

~~~

Do you want to learn a fast and neat way to factor a number? Try the vertical method. Start with the number on the left. On the right, find the smallest prime that is the factor of that number. On the left, write the product of their division below the original number. Write the smallest prime that is a factor of the new, smaller number, on the right. Carry on until the product of division is 1. You found all the factors, in order from the smallest to the largest.