Circles, circles

(More on Brilliant)

The figure below is made of a circle and three semicircles. The white semicircle has the square diagonal as its diameter. The semicircle containing the yellow "moon" has the side of the square as its diameter. And the blue circle has as its diameter the altitude of the equilateral triangle made on the side of the square. If the area of the blue semicircle is 3, can you find the area of the yellow moon?

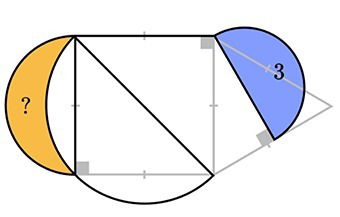
This is a geometrical problem. The first step that I would recommend to my students is to mark all vertices clearly and emphasize any other facts they see that might be useful (e.g., congruent sides and angles, right angles etc). You can see that I also marked the semicircles as #1-3 so that it is easier to describe them.

Since we are discussing the areas of circles and their parts, the key formula that we will use is the area of a circle: A = π * r^2 = π * (d/2)^2 = π * d^2 / 4:

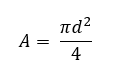
And we are dealing with semicircles, so we will need only a half of the area:

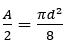
Let's approach this problem starting with the facts that we know. We know the area of the blue semicircle. It can be expressed as A = π * BE^2 / 4 and it is given that it equals 3:

Notice that BE is the altitude of an equilateral triangle with all sides equal BC. We know that BC = 2CE. Using the Pythagorean theorem,

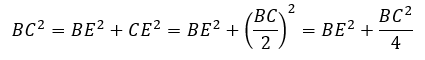
Let's isolate BC and evaluate it using the measure of BE previously found:

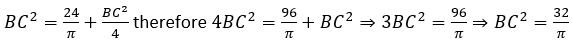
Notice that BC = AD, therefore, we can now find the area of the entire semicircle #2, which includes the yellow moon:

Isn't it neat? Pies canceled and we have a nice, simple area of 4 units.

But we still need to subtract a segment that belongs to the semicircle #1. Lets find the area of #1. Its diameter is the diagonal of a square which sides we found. Using the Pythagorean theorem again,

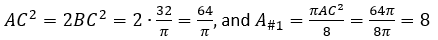
The biggest semicircle, #1, turns out to be twice the size of the smaller semicircle, #2.

The biggest semicircle includes a triangular part, which measures one half of the square area, and two segments of an equal size. Let's find the area of a segment that we will be subtracting from the semicircle #2:

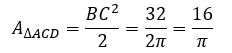
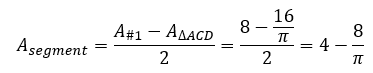
And now that we know the area of the semicircle #2 and the area of the segment that must be subtracted, it is easy to find the answer:

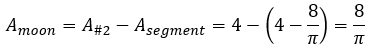
Let's sum up the strategy:

• Mark all vertices and any relevant facts (e.g. congruent sides and angles, angle and segment measures, etc) clearly
• Work step by step starting from the known facts
• Try to use the commonality, e.g. the formula for the area of a circle, since we have three semicircles on the picture and the only known information is the area of one semicircle

Come next week for more!