Heroines of Mathematics - Math Accomplished

By Lito Vilisoni Wilson, University of Melbourne

Some of the prominent mathematicians of the University of Melbourne were asked to share who their favorite math heroines are and why.

Florence Nightingale

(Nominated by Dr Kim-Ahn Le Cao, senior Lecturer In Statistical Genomics, school of Mathematics and Statistics)

Florence Nightingale was far more than a Lady with a Lamp, she was also a talented and creative statistician. She had a natural skill for classifying, analyzing and documenting data.

Florence Nightingale wanted to understand why soldiers in hospital were dying unnecessarily. While she was managing the hospital at the barracks of Scutari in Istanbul during the Crimean war, she recorded the number of soldiers who died from preventable causes compared to wound battles.

Back in Great Britain she analysed her data and invented the polar area diagram (also called Nightingale Rose) to display seasonal sources of patient mortality in Scutari. It also showed how the death rate fell from 46 per cent to 2 per cent when sanitary conditions were improved.

By using data as evidence, and a powerful graphic, she was able to convey to the Members of Parliament and civil servants that sanitation strategies are effective. Florence Nightingale is considered a pioneer in the graphical representation of statistics, which she used “‘to affect thro’ the Eyes what we fail to convey to the public through their word-proof ears’.”

As a highly skilled statistician, she was able to look at data, draw conclusions, create a picture of the results and influence policy.

Florence Nightingale was the first woman to be elected at the Royal Statistical Society in 1859, and became an honorary member of the American Statistical Association in 1874. Her polar diagram plots are still used today.

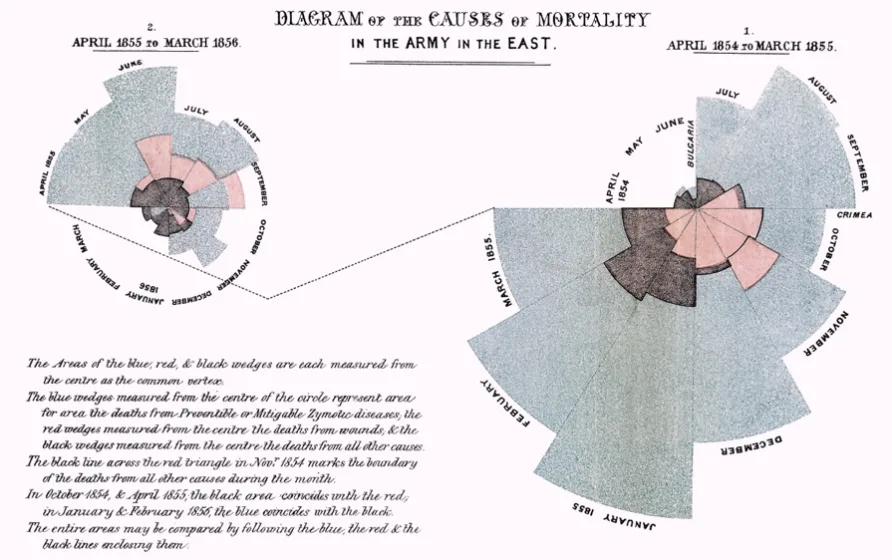
The polar area diagram invented by Florence Nightingale. It shows the number of soldiers deaths (in blue) from preventable cause, those from wounds (red) and other illnesses (black) for each month of the year. Left shows the year 1855-1856 and right 1854-1855. Picture: Supplied

Florence Nightingale urged the Royal Commission to improve sanitary conditions and reduce the number of deaths due to preventable causes in soldiers hospital.

Sofia Kovaleskaya

(Nominated by Dr Jennifer Flegg, Senior Lecturer, School of Mathematics and Statistics)

My favorite female mathematician is Sofia Kovalevskaya, who was born in 1850 in Russia at a time when Russian universities didn’t officially allow women to attend.

Determined to pursue advanced studies in mathematics, she married a man also pursuing an academic career of his own, which allowed her to travel to Germany with him.

In Germany, she was able to informally take classes in mathematics and physics. In 1874 she presented significant mathematical contributions across three different papers that earned her a doctorate, a first for women (in any discipline) at a European university.

Sofia was an amazing pioneer for women in mathematics. Not only was she the first woman to earn a doctorate in Europe, she went on to secure a professorship, another first for women in modern times in Europe. She served as an editor for Acta Mathematica, which remains a prestigious journal in mathematics to this day.

Sofia worked on many things including the theory of partial differential equations and the existence of solutions to these types of equations. This is something that I still use in my applied mathematics research into the mathematical modelling of tissue repair in skin wounds.

Alison Harcourt

(Nominated by Professor Kate Smith-Miles, ARC Georgina Sweet Australian Laureate Fellow, School of Mathematics and Statistics)

My favorite female mathematician is our very own Alison Harcourt (Nee Doig), who I nominated for an UoM honorary doctorate and Order of Australia, both awarded in 2019.

Known in the media as ‘Australia’s ground breaking grandmother of mathematics’, she wrote the paper “An Automatic Method of Solving Discrete Programming Problems”, which is well-known to researchers in the field of optimization.

This seminal paper proposed a method for solving integer programming problems which later became known as the “branch-and-bound” method, and has almost 3000 Google Scholar citations. Most people aren’t aware though that it was authored by two women since their first names are never identified on the paper.

Alison co-authored the paper while working in London as a research assistant to Ailsa Land at the London School of Economics. Alison never enrolled in a PhD, had career interruptions for child-raising and, by the mid-1960s returned to the University of Melbourne to take up a position as a Senior Lecturer in Statistics.

Alison Harcourt is still a tutor in mathematics and statistics at The University of Melbourne at the age of 89. Picture: Supplied

As a statistician, Alison’s analyses have had profound impacts influencing government policy. Examples include the first attempts to estimate poverty in Australia (informing the Royal Commission of Inquiry into Poverty); and statistical analysis of bias that lead to an amendment of the Commonwealth Electoral Act in 1984 which introduced a “double randomization” method for allocating positions of political parties on ballot papers which is still used today.

She formally retired as a Senior Lecturer in 1994 and was awarded an honorary doctorate last year. She continues to share her passion for teaching as a sessional tutor in mathematics and statistics at The University of Melbourne at the age of 89!

Emmy Noether

(Nominated by Professor Jan de Gier, Head of the School of Mathematics and Statistics)

For me it is Emmy Noether because she is close to my area of research, which is mathematical physics, (non-equilibrium) statistical mechanics and combinatorics, and because of her perseverance in a time where women were largely excluded from academic positions.

Noether’s theorem, linking symmetry to conserved quantities in physics and differential calculus has been called “one of the most important mathematical theorems ever proved in guiding the development of modern physics”.

Noether’s theorem from her early work laid bare the deep connection between symmetry and classical mechanics, and had a profound effect on quantum mechanics and later quantum field theory. Symmetries are described by mathematical concepts called ‘groups’, such as the ‘group of rotations in three dimensions’, and related structures called ‘algebras’.

My work in mathematical physics uses structures like ‘Hopf algebras’ and ‘quantum groups’ to derive universally valid formulas from mathematical models that describe transport phenomena in a wide range of contexts, such as in percolation, road traffic, coffee stain growth and single file diffusion in DNA translocation.

‘Groups’ and ‘algebras’ are sets of axioms (established truths) and rules that mathematicians use to deal with abstract symmetries. These can manifest in many different ways, such as symmetries occurring in the standard model of particle physics, rotation symmetries of Rubik’s cube, or underlying mathematical models that allow for deep analysis to unravel fundamental truths about our world.

Noether also had a profound influence on the theory of ‘rings’, another set of axiomatic rules.